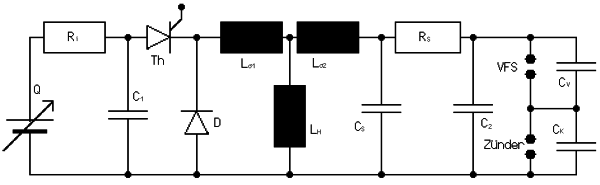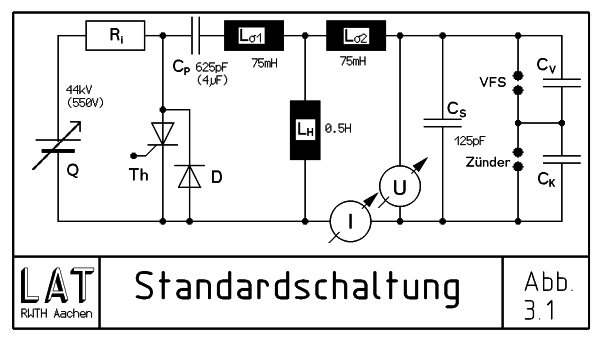
Alle motorischen Messungen erfolgten mit einem vom IOB [1] zur Verfügung gestellten Versorgungssystem.

|
| Abb. 3.1 Standardschaltung |
Zur Verdeutlichung der elektrischen Vorgänge wird hier die in der Elektrotechnik allgemein übliche umgerechnete Ersatzschaltung [2] verwendet. Abweichend von der sonstigen Gepflogenheit wurde die Primär- auf die Sekundärseite umgerechnet. Die tatsächlichen Bauteilwerte der Primärseite sind im Klammern zusätzlich mit aufgeführt. Zur Messung der Vorgänge wurden zwischen Zündspule und Zünder die beiden gezeigten Meßgeräte eingefügt. Als Spannungsmesser diente ein Tektronix 1:1000 Tastkopf, der zusammen mit dem verwendeten Oszilloskop auf den relevanten Frequenzbereich 10 ÷ 50 kHz abgeglichen wurde. Zur Strommessung wurde in die Masseleitung ein 10 Ω- Widerstand eingeschleift und der Spannungsabfall oszilloskopiert. Der Gesamtvorgang gliedert sich nun in vier Etappen:
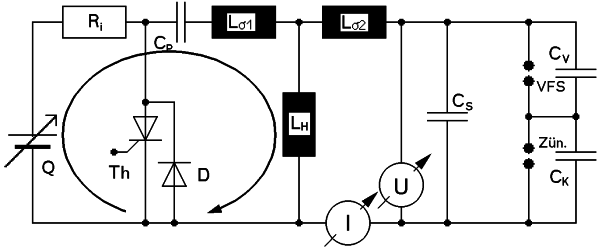
Die einstellbare Quelle lädt begrenzt durch ihren Innenwiderstand Ri den Primärkondensator CP. Geschlossen wird der Stromkreis über die Primärseite der Spule Lσ1 und LH. Zum Ausgleich aller aufbaubedingten Verluste und Erzielen einer hohen Zuverlässigkeit wurden im allgemeinen 6 μF, 450 V oder 4 μF, 550 V entsprechend jeweils 600 mJ primär gespeicherter Energie gewählt.
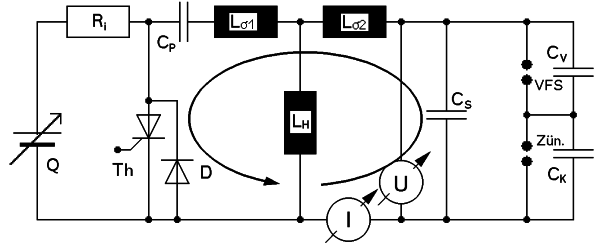
Nach Zündung des Thyristors Th entlädt sich über die Streuinduktivitäten der Spule Lσ1 und Lσ2 der Primär- in den Sekundärkondensator CS. Der Startpunkt liegt dabei im Stromnullpunkt des so gebildeten L-C-Schwingkreises. Dessen Frequenz liegt bei 40 kHz und ohne Durchbruch würde das Spannungsmaximum des Sekundärkondensators nach 12 μsec erreicht.
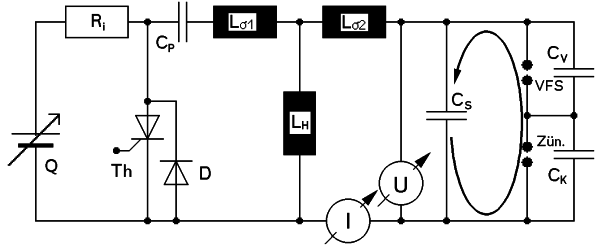
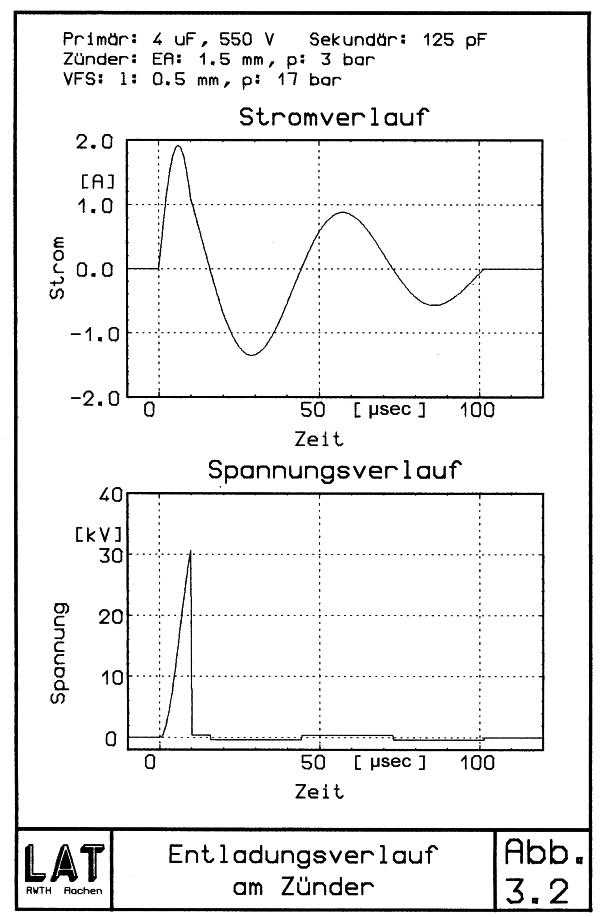
Bei ca 17 kV ist die Durchbruchspannung der Zünderspitze erreicht. Dies ermöglicht die Entladung der parasitären Kapazität der Vorfunkenstrecke CV. Der Effekt ist erkennbar an einem leichten Einbruch in der Spannungskurve. Bei etwa 31 kV bricht die Vorfunkenstrecke durch. Die nun folgende Entladung des Sekundärkondensators über die beiden Funkenstrecken verläuft völlig im Inneren des Zünders und ist deshalb mit den gezeigten Meßgeräten nicht darstellbar. Dies gilt auch für den Spannungsverlauf, da die Geschwindigkeit des Zusammenbruches erheblich über der nutzbaren Grenzfrequenz des Hochspannungstastkopfes liegt.
Die Entladung des Sekundärkondensators hinterläßt die beiden Funkenstrecken in ionisiertem und damit leitendem Zustand. Damit ist der Stromkreis über Cp, Th, die Entladungsbögen und Lσ geschlossen. (Die Ströme über Cs sind wegen der geringen Bogenspannung von ca. 400 V vernachlässigbar.) Die Frequenz des von CP und Lσ gebildeten Schwingkreises liegt bei 17 kHz. In diesem Nachfunken entlädt sich die im Durchbruchsmoment im Primärkondensator noch enthaltene Energie. Nach meistens 4 Halbwellen sperrt der Thyristor. Abb. 3.2 zeigt den gemessenen Strom und Spannungsverlauf. Die in den beiden Bögen im Nachfunken umgesetzte Energie liegt als Integral des Produktes von Spannung und Strom damit bei 30 mJ. Nach der vierten Halbwelle ist der Primärkondensator wieder auf etwa 140 V Restspannung entsprechend 40 mJ aufgeladen. Diese sind von den anfangs gespeicherten 600 mJ abzuziehen. Der resultierende primäre Energieeinsatz liegt also bei 560 mJ.
|
| Abb. 3.2 Entladungsverlauf am Zünder |
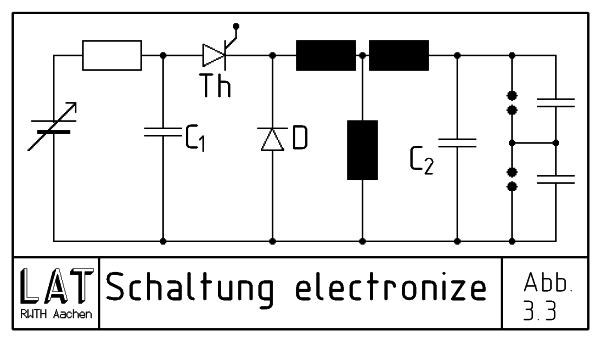
Für die kalorimetrische Messung der Energieübertragung erwies sich die am Prüfstand verwendete Energieversorgung als unbrauchbar. Den theoretischen Überlegungen entsprechend waren bei der Auswertung der motorischen Versuche [3] bislang nur die im Sekundärkondensator gespeicherten Energien betrachtet worden. Der in Kap. 3.1.4 beschriebene Nachfunke setzt jedoch wie beschrieben noch einmal ca. 30 mJ an elektrischer Energie um, und damit fast genau so viel wie in den kleineren Kondensatoren gespeichert wird. Eine Unterdrückung dieses Nachfunkens ist mit der oben beschriebenen Schaltung prinzipiell nicht möglich. Für die kalorimetrischen Messungen wurde daher eine handelsübliche britische Kondensatorzündung der Firma electronize design aus Sutton Coldfield adaptiert. Abb. 3.3 zeigt die resultierende Ersatzschaltung:
|
| Abb. 3.3 Schaltung electronize |
Der verlustlose Ablauf sieht nun so aus:
Im Auslösemoment sind sowohl der Strom als auch die Ladung in C2 gleich Null, C1 ist geladen. Durch den Thyristor Th beginnt ein von den Streuinduktivitäten begrenzter Strom zu fließen. Die steigende Spannung auf C2 und die fallende auf C1 verlangsamen den Stromanstieg bis sich bei Spannungsgleichheit U(C1*)= U(C2) [4] die Kondensatoren im Gleichgewicht befinden. Zu diesem Zeitpunkt hat der Strom sein Maximum erreicht und damit die maximale Energie in den Streuinduktivitäten Lσ1 und Lσ2 gespeichert. Diese bewirken sein Weiterfließen und ein weiteres Aufladen von C2 bis in dessen Spannungsmaximum der Strom wieder zu Null wird. Falls jetzt genau C1*=C2 gilt, so ist die Spannung U(C1)= 0, und die gesamte Energie befindet sich im Sekundärkondensator. Solange C1*>C2 kann jedoch C1 bei diesem Vorgang nie vollständig entladen werden und entlädt zwangsläufig seine Restenergie im Nachfunken. Die Bedingung C1*= C2 ist natürlich praktisch kaum zu verwirklichen. Wir wählen daher C1*< C2. Dadurch wird U(C1)= 0 schon vor dem Spannungsmaximum auf C2 erreicht und der weiterfließende Strom lüde ohne die Diode D den Kondensator C1 negativ auf, wobei natürlich ebenfalls Energie in C1 gespeichert würde. Negative Spannungen werden jedoch von D kurzgeschlossen und C1 dadurch vollständig entladen. Eine gewisse Restenergie in Lσ wird sich im Durchbruchsmoment jedoch nicht vermeiden lassen. Nun ist aber die Induktivität eine Stromquelle und die Stromstärke der geringen Restenergie liegt unter dem Mindesthaltestrom der Funkenstrecken. Die Entladung verlischt also und die Restenergie wird von C2 aufgenommen, ohne daß es bei der geringen Spannung zur erneuten Zündung kommen kann. Ein Problem bei den Messungen war die Notwendigkeit, mit zwei verschiedenen Spulen zu arbeiten. Obwohl es sicher optimal gewesen wäre bei jedem Wechsel des Sekundärkondensators den Primärkondensator jeweils anzupassen, war dies Verfahren unpraktikabel. Zuverlässiges Arbeiten mit der größten Kapazität von 210 pF erforderte mindestens 1 μF primär und eine Spule mit geringen Verlusten. Verwendet wurde die "rote Hochleistungsspule" Bosch Nr: 0 221 119 030 mit einem Übersetzungsverhältnis von ü = 100. Wegen C1*= C1/ü² ≈ 100 pF wurde für die beiden kleinsten Kondensatoren mit 54 pF und 34 pF auf die alte Bosch Transistorspule Nr: 0 221 122 001 mit ü = 150 zurückgegriffen. Für sie gilt C1* = C1/ü² ≈ 44 pF [5]
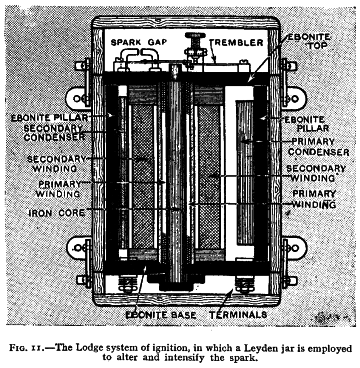
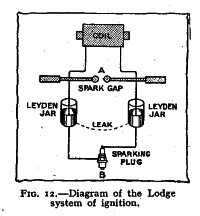
In der Literatur werden für die Energieumsetzung der drei Phasen einer induktiven Funkenentladung sehr unterschiedliche Werte genannt. So soll der Wirkungsgrad 95 % im Durchbruch aber nur etwa 40 % bzw. 25 % bei Bogen- und Glimmentladung betragen. Der Konstruktion des Zünders lag daher die Hoffnung zugrunde, durch Minimierung der Eigeninduktivität Entladungszeiten im Nanosekundenbereich und eine Freisetzung fast der gesamten Energie in der Durchbruchsphase zu erzielen. Der Versuch, mit Hilfe von Hochspannungskondensatoren auf der Sekundärseite zu einem besonders intensiven Funken zu gelangen, ist nicht neu. Bereits vor 1926 wurde von Sir Oliver Lodge, F.R.S. ein solches System in Serie produziert /Hu26/. Abb. 3.4 zeigt den Aufbau und die Schaltung.
|
|
| Abb. 3.4 Aufbau und Schaltung des Lodge Stoßentladungszünders /Hu26/ | |
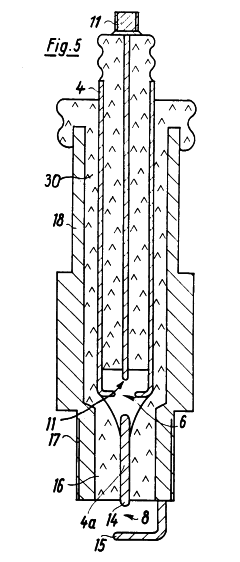
Die wichtigsten Komponenten - Vorfunkenstrecke und Hochspannungskondensator - sind vorhanden, die Bedeutung der Leitungsinduktivitäten und -verluste mit der Notwendigkeit den Kondensator möglichst nahe an der Kerze zu positionieren wurde jedoch offenbar noch nicht erkannt und die Komponenten im Gehäuse der Zündspule untergebracht. Es wurden dennoch mit ca. 1 MHz bereits Entladungsfrequenzen erzielt, die den von Kupe 1988 erreichten 5 MHz praktisch gleichkommen. Weder Lodge noch Kupe sprachen denn auch von einer Durchbruchs- sondern von einer Höchststrom-Bogenenentladung. Die Energieübertragung im Durchbruch wird von Bloss für seine 1978 zum Patent [6] angemeldete Zünderversion in Anspruch genommen. Abb. 3.5 zeigt eine von ihm vorgestellte Bauart.
|
| Abb. 3.5 Durchbruchszünder nach Bloss /Bl78/ |
Mit den Maßen der Zeichnung [7] und dem in der Beschreibung erwähnten Al2O3 als Dielektrikum liegt die Kapazität bei 50 pF. Die Spannung dürfte wie bei unseren Versuchen bei gut 30 kV und die gespeicherte Energie damit bei 25 mJ liegen. Der Verlauf des elektrischen Durchbruches ist von Hess 1976 quantitativ beschrieben worden /He76/. Für die Halbwertsbreite der Entladung gilt danach
| mit: | d = 2 mm |
| p = 4 barabs | |
| a = 1•10-4 (bar•m²)/(V²•sec) | |
| U = 32 kV | |
| gilt: | tH ≈ 0.5 nsec |
Der Elekrodenabstand d kann im praktischen Betrieb kaum größer als 2 mm gewählt werden [8]. 4 barabs ist ein typischer Zylinderdruck und die Konstante a ist aus /He76/ übernommen. Damit erfolgt die Entladung mit Frequenzen oberhalb mindestens 500 MHz. Die Resonanzfrequenz des Zünders muß, um die Entladung nicht zu behindern, um wenigstens eine Größenordnung darüber, also bei 5 GHz, liegen. Die zulässige Induktivität beträgt dann maximal 0.02 nH. Allein die Induktivität des Verbindungsstiftes "4a" zwischen den beiden Funkenstrecken ist mit ca. 5 nH um etwa den Faktor 200 größer.
Im wesentlichen waren zur Messung der Stoßentladung zwei Schwierigkeiten zu überwinden:
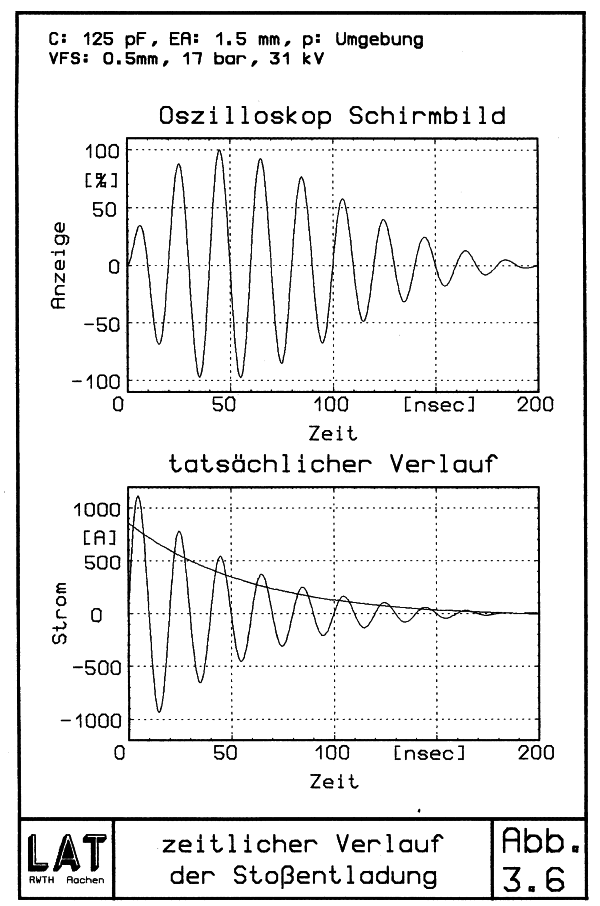
Da hier nicht versucht werden sollte, die Entladungsströme zu messen, sondern nur ihren Verlauf zu beobachten, konnten beide Schwierigkeiten umgangen werden. Der Rückstrom zur Massefläche des Sekundärkondensators fließt im Gehäusemantel des Zünders. Die erwartete Stromstärke von einigen hundert Ampere sollte über dem Zünderhals also durchaus einen meßbaren Spannungsabfall verursachen. An beiden Enden des Halses wurden daher Abgreifpunkte aufgelötet. Schwieriger war die Wahl eines brauchbaren Meßgerätes. Alle von der Bandbreite her geeigneten Oszilloskope erwiesen sich als viel zu störanfällig. Schon bei offenen und intern geerdeten Eingängen zeigte sich ein bildschirmfüllendes Signalgemisch. Als geeignet erwies sich schließlich ein älteres Philipps PM 3232 mit nur 10 MHz Bandbreite. Offenbar machte der einfache innere Aufbau es weniger anfällig für Einstreuungen in spätere Verstärkerstufen. Damit lag das Meßsignal zwar deutlich oberhalb der Grenzfrequenz, für eine reine Beobachtung der Grundwelle unter Verzicht auf die Bestimmung der Kurvenform und Amplitude war das Gerät jedoch ausreichend. Um sicher zu sein, tatsächlich Eigenschaften des Objektes und nicht des Meßgerätes zu bestimmen, wurden zwei sehr unterschiedliche Aufnehmer verwendet. Zum einen war dies ein beidseitig mit dem Wellenwiderstand von 50 Ω abgeschlossenes und direkt aufgelötetes Hochfrequenzkabel und als zweites ein handelsüblicher 1:10 Tastkopf. Jeweils der eine Aufnehmer wurde zur Triggerung und der andere zum Signalabgriff verwendet. In beiden Fällen ergab sich identisch das in Abb. 3.6 dargestellte Schirmbild.
|
| Abb. 3.6 zeitlicher Verlauf der Stoßentladung |
Man erkennt deutlich eine Schwingung von 50 MHz, die in etwa 200 nsec abklingt. Der Anstieg in den ersten 60 nsec ist offenbar auf Einschwingvorgänge im Meßgerät zurückzuführen. Mit Hilfe der bekannten Ladung im Kondensator von
Q = 125 pF • 31 kV = 3.9 μC,
die in einer Sinusviertelwelle abfließt, erhalten wir den in Abb. 3.6 unten dargestellten tatsächlichen Stromverlauf. Das Auftreten dieser Oszillationen setzt natürlich das Vorhandensein einer hinreichend großen Induktivität voraus. Ihre Größe ergibt sich aus:
Für die Induktivität koaxialer Kabel gilt:
| mit: | l: Leiterlänge |
| D: Innendurchmesser des Außenleiters | |
| d: Außendurchmesser des Innenleiters |
Setzt man als ungefähre Werte des Zünderhalses ein:
l = 150 mm
D = 30 mm
d = 4 mm
so finden wir
L ≈ 60 nH
in guter Übereistimmung zum gemessenen Wert.
Vorbereitend für die motorischen Zünderuntersuchungen war als erstes der Einfluß des in Kap. 3.1.4 beschriebenen Nachfunkens auf den Motorbetrieb zu untersuchen. Messungen in der Druckkammer ergaben für ihn etwa 30 mJ elektrische Energie. Davon werden mehr als 10 mJ ans Gas abgegeben. Schon beim zweitgrößten Kondensator mit 125 pF sind das 55 % der bei der Entladung freigesetzten Energie. Wenn, wie in der Theorie vorhergesagt, die Zündung vor allem auf dem vom Sekundärkondensator gespeisten Plasmaeffekt beruhen soll, dürfte der Nachfunke dennoch keinen meßbaren Einfluß mehr haben [9]. Es wurde also derselbe Meßpunkt im Motor unmittelbar nacheinander einmal mit der üblichen Energieversorgung und einmal mit der in Kap. 3.3.2 beschriebenen aufgenommen [10]. Abb. 3.7 zeigt die Ergebnisse und Abb. 3.8 die Auswertung der resultierenden Brennfunktionen. Die Übereinstimmung der Meßpunkte ist deutlich besser, als die Reproduzierbarkeit desselben Punktes an verschiedenen Tagen. Die Berechtigung der schon von Brünken und Somuncu gewählten Auswertung, nur die im Kondensator gespeicherte Energie zu berücksichtigen, ist hiermit nachgewiesen [11]. Gleichzeitig zeigt das völlige Fehlen jeglichen Einflusses noch einmal, daß bei der Plasmazündung neue Effekte auftreten, die sie von konventionellen Systemen grundlegend unterscheiden.
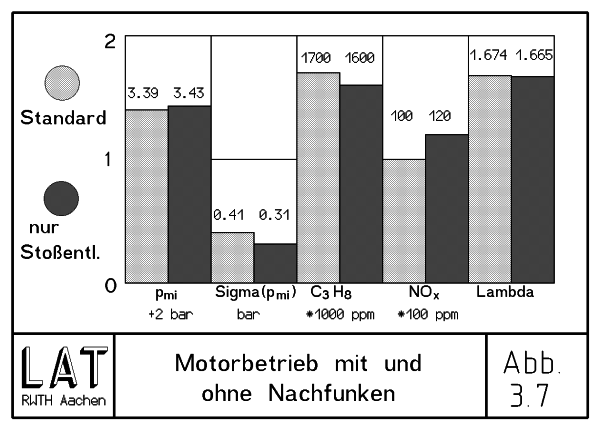
|
| Abb. 3.7 Motorbetrieb mit und ohne Nachfunken |

|
| Abb. 3.8 Brennfunktionsvergleich - Punkte gleichen Umsatzes |
Weiter Inhaltsverzeichnis Übersicht Wissenschaft Home & Impressum