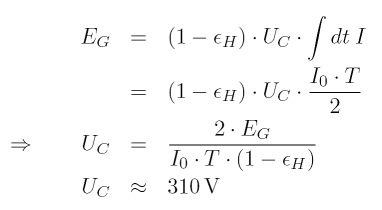
In Abb. 3.6 wurde der der ungefähre Verlauf des Entladungsstromes gezeigt. Genau bekannt sind dabei die Frequenz und (aus der Kondensatorladung) die Höhe des ersten Strommaximums. Die Gesamtdauer der Entladung ist dagegen wegen des offensichtlichen Ein- und damit wohl auch Ausschwingvorganges nur näherungsweise bekannt. Zur Vereinfachung wollen wir im folgenden mit der effektiven Stromstärke des Wechselstroms rechnen. Für eine erste Abschätzung nehmen wir einen linearen Stromabfall in 150 nsec und Verluste im Zünderhohlraum von 5 % [1] an. Der ans Gas abgegebene Energieanteil ist gemäß den Überlegungen von Swett /Sw56/, experimentell bestätigt von Ziegler /Zi90/ genau der in der positiven Säule umgesetzte Teil. Die Energie der Elektrodenfälle und des kathodischen Übergangsgebietes wird von den Elektroden abgeleitet. Damit erhalten wir die mittlere Spannung UC der positiven Säule aus:
| mit: | Kalorimeterenergie: | EG = 18 mJ |
| Anfangsstrom: | Io = 860 A | |
| Entladungsdauer: | T = 150 nsec | |
| Hohlraumverluste: | εH = 0.05 |
Diese Spannung liegt um drei Größenordnungen über der des stationären Gleichstrombogens bei gleicher Stromstärke /Su39a/ /Su39b/. Ursache dafür ist bei der Frequenz von 50 MHz der Skineffekt. Bei hohen Frequenzen fließt der Strom nicht im gesamten Querschnitt eines Leiters, sondern nur in einer dünnen Oberflächenschicht. Bei Gasbögen ist der Effekt vermutlich noch deutlich ausgeprägter als bei homogenen festen Leitern. Die Stromverdrängung aus dem Leiterinneren und damit die Schichtdicke hängt von der Leitfähigkeit im Inneren des Leiters ab, im Gas also des hoch ionisierten Kanalzentrums. Für die Schichtdicke gilt:
| mit: | f: | Frequenz (50 MHz) |
| μo: | abs. Permeabilitätskonstante (1.26⋅106 V⋅sec/(A⋅m)) | |
| μr: | rel. Permeabilität (normalerweise 1) | |
| σi: | Leitfähigkeit im Leiterinneren |
Der Widerstand des Leiterabschnittes ergibt sich aus der Leitfähigkeit der Leiterrandschicht zu:
| mit: | l: | Leiterlänge |
| d: | Leiterdurchmesser | |
| σa: | Leitfähigkeit der Leiterrandschicht |
Für homogene feste Leiter gilt natürlich stets σa = σi, bei Plasmakanälen dagegen vermutlich σa << σi. Zusätzlich ist im Gas der Leiterdurchmesser nicht fest vorgegeben.
Die gemessenen Energien für die Zünderstrecke und Vorfunkenstrecke ergeben zusammen etwa 50 % der gespeicherten Energie. Als wichtigste Verlustterme wollen wir die ohm'schen Verluste des Zünders und die dielektrischen Verluste des Kondensators betrachten. Der ohm'sche Widerstand wird wesentlich durch den Skineffekt bestimmt. Der Widerstand des Mantels ist wegen des erheblich größeren Umfangs gegen den des Mittelleiters vernachlässigbar. Die verwendeten Materialien sind Messing für den Zünderhals, VA-Stahl für die Einstellschraube und Wolfram in der Zünderspitze. Wir finden mit Gleichung (5.2) und (5.3):
| Zünderhals: | σMS | = | 15⋅106 (Ω⋅m)-1 |
| δMS | = | 18 μm | |
| l | = | 105 mm | |
| R | = | 0.03 Ω | |
| Einstellschraube: | σVA | = | 10⋅106 (Ω⋅m)-1 |
| δVA | = | 22 μm | |
| l | = | 25 mm | |
| R | = | 0.014 Ω | |
| Mittelelektrode: | σW | = | 18⋅106 (Ω⋅m)-1 |
| δW | = | 16 μm | |
| l | = | 75 mm | |
| R | = | 0.02 Ω | |
| Summe: | Σ(R) | = | 0.065 Ω |
Der ohm'sche Gesamtverlust kann daher mit
RR ≈ 0.1 Ω
abgeschätzt werden.
Die dielektrischen Verluste eines Kondensators werden im allgemeinen als Tangens des Verlustwinkels tgδ bzw. dessen Kehrwert die Kondensatorgüte Q ≡ (tgδ)-1 angegeben. Der reale Kondensator läßt sich (unter Vernachlässigung weiterer parasitärer Effekte) als Reihenschaltung aus Widerstand und idealem Kondensator modellieren. Für die Größe des Serienwiderstandes in diesem Modell gilt dann:
als Blindwiderstand des Kondensators.
Für 125 pF und 50 MHz finden wir:
XC ≈ 25 Ω
Der Verlustfaktor tgδ ist im allgemeinen stark frequenzabhängig. Für den hier verwendeten Werkstoff POM (Polyoximethylen, Handelsnamen: Polyacetal, Delrin) sind Werte für Frequenzen oberhalb 1 kHz nicht tabelliert. Der im niedrigen Frequenzbereich recht ähnliche viel verwendete Kondensatorwerkstoff PC (Polycarbonat) weist oberhalb 10 MHz Werte von ca.
tgδ ≈ 0.05
auf. Damit ergibt sich:
RS ≈ 1.3 Ω
und dies scheint der Hauptverlustterm zu sein.
Eine analytische Beschreibung des Entladungsvorganges ist möglich, wenn in der Stromabhängigkeit nur Terme mit U = const. oder R = const. auftreten. Bei Standardzündungen hat es sich bewährt, die Brennspannung als während der Entladung konstant anzusehen. Es sind dann die ohm'schen Verluste proportional zum Quadrat des Stroms ER ∼ I² und die Nutzleistung im Bogen dem Strom direkt proportional EU ∼ I mit der Folge stark stromabhängiger Wirkungsgrade. Die Ergebnisse aus Kap. 4.5.3 zeigen, daß dies hier offenbar nicht der Fall ist. Bei gegebener Kapazität und damit Frequenz ist der Wirkungsgrad praktisch energie- und damit stromunabhängig. Offenbar verlangt ein solches Verhalten die Modellierung des Hochfrequenzbogens als ohm'schen Widerstand [2]. Die Elektrodenfälle dürften bei 50 V pro Funkenstrecke liegen. Der damit eingeführte Konstantspannungsterm führt auf eine endliche Entladungsdauer im Gegensatz zum unendlichen asymptotischen Abfall bei rein ohm'scher Belastung. Als Stromverlauf erhalten wir damit einen exponentiellen Abfall des Anfangsstroms Io auf einen hypothetischen negativen Endstrom
Die Zeitkonstante ist beim Schwingkreis wegen der zwei Energiespeicher L und C doppelt so groß wie beim induktiven Gleichstrombogen:
damit
Selbstverständlich ist diese Beziehung [3] nur für i>0 gültig. Mit der Forderung
i = 0 ⇒ t = T
erhalten wir die Funkenstandzeit:
Für die Energie über einer konstanten Spannung u gilt dann:
und an einem ohm'schen Widerstand r
Die benötigten Integrale lauten:
Der Widerstand der Bogensäule ist proportional zum Elektrodenabstand d. Die Druckabhängigkeit schätzen wir analog zu der des Gleichstrombogens /Su39a/ /Su39b/ mit p0.4 ab:
Im Standardfall haben wir an Vorfunkenstrecke und Zünder:
| dZ | = | 1.5 mm | |
| pDK | = | 4 barabs | |
| dVFS | = | 0.5 mm | |
| pVFS | = | 18 barabs | |
| Damit wird: | RVFS | = | 0.61⋅RZ |
Für den Energieeintrag ins Gas gilt:
Mit:
| Rges | = | RZ + RVFS + 1.4 Ω |
| Uges | = | 100 V |
| εH | = | 0.05 |
| Io | = | 860 A |
| EG | = | 18.1 mJ |
finden wir:
RZ = 1.08 Ω
T = 170 nsec
Für die Bogenwiderstandskonstante gilt damit:
Φ = 0.415 Ω⋅mm-1bar-0.4
und im Normalfall
RVFS = 0.66 Ω
Die Messung in Kap. 3.3.2 war der Einfachheit halber mit drucklosem Zünder durchgeführt worden (pabs=1bar). Einsetzen in (5.13) ergibt:
RZ= 0.62 Ω
T = 190 nsec
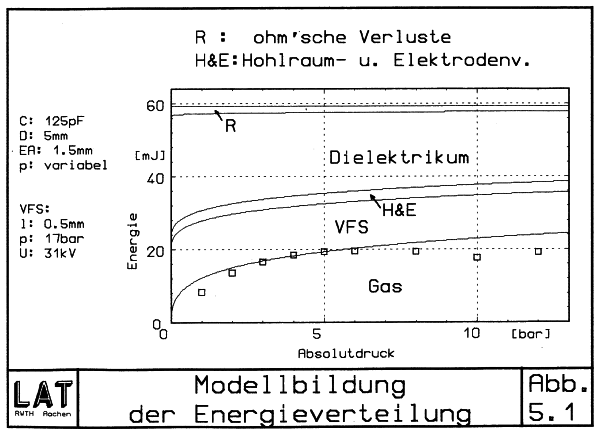
in sehr guter Übereinstimmung zur beobachteten Entladungsdauer [4]. Unter Anwendung dieses Modells ergeben sich die folgenden Energieverteilungen:
Die eingezeichneten Meßpunkte weichen vom theoretischen Verlauf spürbar ab. Nach einem schwächer gekrümmten Anstieg folgt oberhalb 6 bar eine Sättigung. Die Ursache dürfte sein, daß zur Ausbildung einer ungestörten Bogensäule eine Mindestlänge erforderlich ist. Die Elektrodenabstände lagen bei den Experimenten von Suits in der Regel auch bei 10 mm und unterhalb von 4 mm traten Störungen des Bogengradienten auf /Su39a/. Als Folge dürften die Vorfunkenstreckenverluste im Verhältnis zur Nutzenergie etwas zu hoch angesetzt sein [5]. Es wird sich jedoch zeigen, daß die Brauchbarkeit des Modells davon nicht sehr berührt wird.
|
| Abb. 5.1 Modellbildung der Energieverteilung |
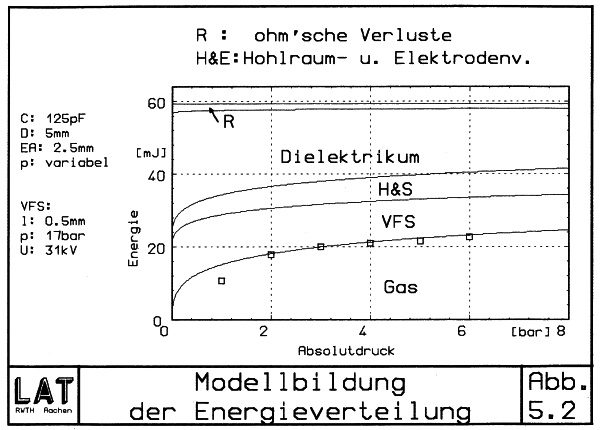
Um beim Kammerdruck p = 4 barabs die gemessene Energie zu erhalten, mußte der Hohlraumverlust mit εH = 19 % angesetzt werden. Mit Ausnahme des Punktes bei Umgebungsdruck ist die Übereinstimmung mit dem Meßwerten bei diesem größeren Elektrodenabstand ausgezeichnet. Die Messungen ohne Vorfunkenstrecke können wegen der sich ändernden Energieanteile in Kondensator und Leiterwiderstand in Abb. 5.2 natürlich nicht mit eingetragen werden.
|
| Abb. 5.2 Energieverteilung mit VFS |
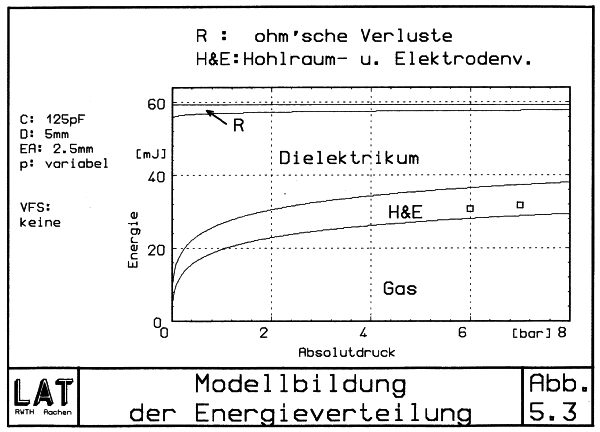
Abb. 5.3 zeigt die Werte unter diesen Bedingungen. Offenbar werden die beiden Meßwerte nicht gut getroffen. Denkbar wären neben geringeren Vorfunkenstreckenverlusten auch kleinere Hohlraumverluste von nur εH≈11%. Wie in Kap. 4.3 gezeigt ist aufgrund höherer Energie ein schnellerer Ausstoß mit geringeren Wandverlusten immerhin denkbar.
|
| Abb. 5.3 Energieverteilung ohne VFS |
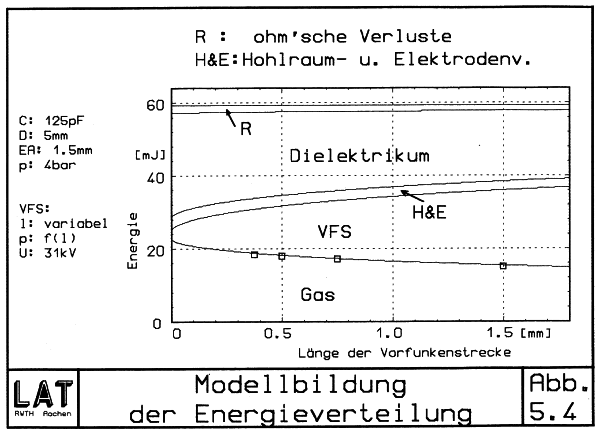
Bei Variation der Vorfunkenstrecke unter Konstanthaltung der Durchbruchspannung gilt wie gezeigt (Kap. 4.5.2) das Paschen Gesetz
pabs⋅d = const. = 9 bar⋅mm
Beziehung (5.13) vereinfacht sich damit zu
RVFS = 1.00 Ω⋅mm-0.6⋅d0.6
Es ergibt sich die folgende Energieaufteilung in guter Übereinstimmung zu den Meßwerten.
|
| Abb. 5.4 Energieverteilung bei variabler VFS |
Bisher haben wir nur den Fall mit C = 125 pF, f = 50 MHz betrachtet. Für die Frequenz gilt:
Für konstantes L also:
Falls:
tgδ ≈ const.
(bei geringen Frequenzänderungen ist das in der Regel korrekt) gilt für die dielektrischen Verluste (5.4)
bzw. mit (5.16)
(5.18) RS ∼ f
Für die ohm'schen Verluste gilt nach (5.2) und (5.3)
RR ∼ √f
Wegen RR << RS verwenden wir jedoch vereinfachend näherungsweise:
(RR + RS) ∼ f
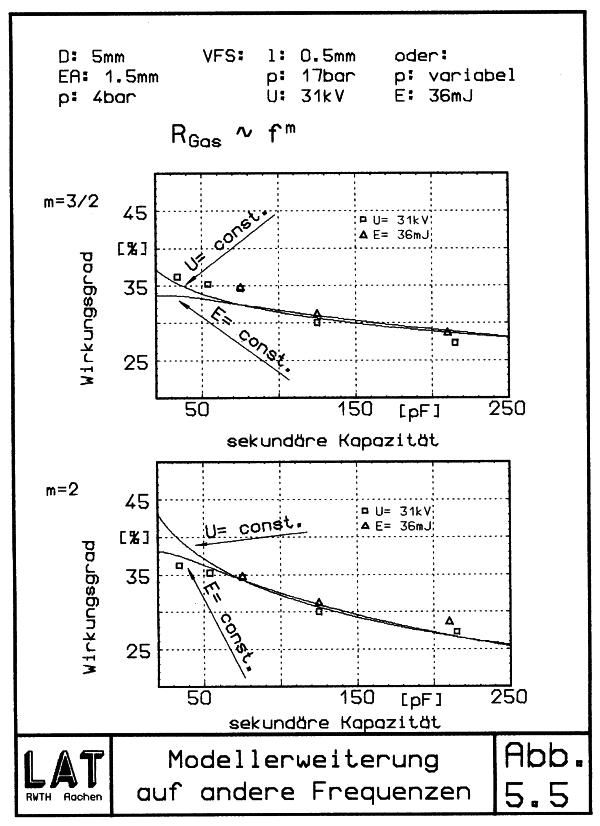
Da bei höheren Frequenzen der Wirkungsgrad steigt, muß sich Φ mit f stärker als proportional ändern. Eine passable Näherung scheint zu sein:
Φ ∼ fm
mit 3/2 < m < 2. Abb. 5.5 zeigt den Vergleich zu gemessenen Werten.
|
| Abb. 5.5 Modellerweiterung auf andere Frequenzen |
Das hier vorgestellte Modell ist ein Versuch, die Energieverteilung auf die wichtigsten Verlustterme darzustellen und qualitativ zu erklären. Angesichts der Übereinstimmung mit gemessenen Werten, kann dies im wesentlichen als gelungen angesehen werden. Die Einflüsse der Parameter:
werden qualitativ richtig wiedergegeben. Damit ist eine systematische rechnerische Auslegung der nächsten Zündergeneration möglich geworden. An die quantitative Genauigkeit des Modells dürfen dagegen keine zu hohen Ansprüche gestellt werden. Die Gründe sind:
Weiter Inhaltsverzeichnis Übersicht Wissenschaft Home & Impressum